Home - Sokheng Din

The Optimal Control Theory in Control System

Optimal Control is a branch of control theory in control system, the theory works by solving the optimization problem of the dynamical system in order to find the optimal solution for the system

What is Model Predictive Control ?

Model Predictive Control (MPC) is the optimal control method that use optimization algorithms to solve the cost function the occurs from the desired input and obtain back the optimal input control over the finite and infinite horizons. Recently, MPC is hyping up among the control system researcher, since it is fast, efficiency and robustness for any high complex system.

Hamilton Jacobian Bellman Equation (HJBE)

Actually, the HJBE is a nonlinear partial differential equation that it consists necessary conditions for optimality of control by minimizing the loss function of the system.

We have the Hamiltonian Jacobian Bellman Equation

\begin{equation*} H(x,u,\lambda,\mu) = \sum_{k=0}^{N-1}(x_{k}-x_{k,ref})^{T} Q(x_{k}-x_{k,ref}) + (u_{k}-u_{k,ref})^{T}R(u_{k}-u_{k,ref}) + \phi(x) + \lambda^{T}f(x,u) + \mu^{T}C(x,u) \end{equation*}

Which

$N$
is the number of prediction future horizons or shooting node.
$x_{k}$
is the state of the system at shooting node
$k$
.
$u_{k}$
is the input control of the system at shooting node
$k$
.
$Q, R$
are diagonal matrix which helps the optimization solving the nlp problem.
$f(x,u)$
is the state representation of the system.
$C(x,u)$
is the constraint of the system.
$\lambda$
is the costate vector for state representation.
$\mu$
is the Lagrange multiplier vector for the equality constraint.

Nonlinear Model Predictive Control has multiples solving method, but in this demonstration I will stick with the Continuation/GMRES method proposed by professor Toshiyuki Ohtsuka .

Supposed we want to obtain solution vector

U(t) = [ u_{0}^{*}, \mu_{0}^{*}, \cdots, u_{N-1}^{*}, \mu_{N-1}^{*} ]

at sampling time $t$, we then define the discretization of Euler Lagrangian Equation (ELE) .

\begin{align} x_{i+1}^{*}(t) &= x_{i}^{*}(t) + f(x_{i}^{*}(t), u_{i}^{*}(t)) \\ \lambda_{i}^{*}(t) &= \lambda_{i+1}^{*}(t) + \frac{\partial H}{\partial x}\left( x_{i}^{*}, u_{i}^{*}(t), \lambda_{i+1}^{*}(t), \mu_{i}^{*}(t) \right) \\ \lambda_{N}^{*}(t) &= \frac{\partial \phi(x)}{\partial x} \\ \frac{\partial H}{\partial u} &\left( x_{i}^{*}, u_{i}^{*}(t), \lambda_{i+1}^{*}(t), \mu_{i}^{*}(t) \right) = 0 \\ C&(x_{i}^{*}(t),u_{i}^{*}(t)) = 0 \end{align}

To solve this nonlinear problem iteratively, we use Newton's method

F(x,u)=0

\begin{equation*} F(x,u) = \begin{bmatrix} \frac{\partial H}{\partial u} \left( x_{0}^{*}, u_{0}^{*}(t), \lambda_{1}^{*}(t), \mu_{0}^{*}(t) \right) \\ C(x_{0}^{*}(t),u_{0}^{*}(t)) \\ \vdots \\ \frac{\partial H}{\partial u} \left( x_{N-1}^{*}, u_{N-1}^{*}(t), \lambda_{N}^{*}(t), \mu_{N-1}^{*}(t) \right) \\ C(x_{N-1}^{*}(t),u_{N-1}^{*}(t)) \\ \end{bmatrix} = 0 \end{equation*}

Solving this problem directly will caused big computational complexity, hence we use Continuation to reduce the complexity of the

F(x,u)

function and then solve it by using GMRES method.

Continuation

Denote

\zeta, \alpha, h \in{\mathbb{R} }

\begin{equation*} \frac{\partial F}{\partial u}(x,u) \dot{u}(t) = -\zeta F(x,u)(t)-\frac{\partial F}{\partial x}(x,u)(t)\dot{x}-\frac{\partial F}{\partial t}(x,u)(t) \end{equation*}

Let

right=\frac{F(x(t)+h\dot{x}(t),u(t)+h\dot{u}(t),t+h)-F(x+h\dot{x}(t),u(t),t+h)}{h}

and

left = -\zeta F(x(t),u(t), t) - \frac{F(x+h\dot{x}(t), u(t),t+h)-F(x(t), u(t), t)}{h}

Generalized Minimal Residue Method (GMRES)

The Generalized Minimal Residual (GMRES) algorithm is an iterative method for solving linear systems of equations. It is often used for large sparse linear systems.

Algorithm Description

Initialize:
- Choose an initial guess for the solution, denoted as
  $x_{0}$
  .
- Set the residual vector
  $r_{0}=\left\| Ax_{0}-b \right\|$
  .
- Set
  $v_{1}=\frac{r_{0} }{\left\| r_{0} \right\|}$
  , where
  $\left\| r_{0} \right\|$
  is the norm of
  $r_{0}$
  .
Iterative Process:
- Choose a vector
  $v_{1}$
  .
- For
  $k=0$
  to
  $maxiteration$
  :
  - Arnoldi process:
    - $h_{i,j} = \left(Av_{j}, v_{i} \right)$
    - $\hat{v}_{j+1} = Av_{j} - \sum_{i=1}^{j}h_{i,j}v_{i}$
    - $h_{j+1,j} = \left \| \hat{v}_{j+1} \right\|_{2}$
    - $v_{j+1} = \frac{\hat{v}_{j+1} }{h_{j+1,j} }$
  - Check for convergence:
    - If
      $||r_k|| < tolerance$
      , exit the loop.
- If no convergence is achieved after
  $maxiterations$
  , exit with an error message.
Find
$y$
: which minimize
$\left\| r_{0}e_{1}-\hat{H}_{m}y \right \|_{2}$
.
Compute:
$x_{m} = x_{0}+V_{m}y_{m}$
.

For example differential model, let

x, y, \phi

is the state presentation of the model $$ \dot{x} = f(x,u) $$

Then the HJBE defined as

\begin{equation*} H(x,u,\lambda,\mu) = \sum_{k=0}^{N-1}(x_{k}-x_{k,ref})^{T}Q(x_{k}-x_{k,ref}) + (u_{k}-u_{k,ref})^{T}R(u_{k}-u_{k,ref}) + \phi(x) + \lambda^{T}f(x,u) + \mu^{T}C(x,u) \end{equation*}

Which

$f(x,u) = \begin{bmatrix} u_{1}*\cos{(\phi)} \\ u_{1}*\sin{(\phi)} \\ u_{2} \end{bmatrix}$
$C(x,u) = \begin{bmatrix} \left(u_{1}-\frac{u_{1max}+u_{1min}}{2}\right)^{2}+u_{1dummy}^{2}-(\frac{u_{1max}-u_{1min} }{2})^{2} \\ \left(u_{2}-\frac{u_{2max}+u_{2min} }{2}\right)^{2}+u_{2dummy}^{2}-(\frac{u_{2max}-u_{2min}}{2})^{2} \end{bmatrix}$
$\phi(x) = (x_{N}-x_{N,ref})^{T}Q(x_{N}-x_{N,ref})$
$\lambda = \begin{bmatrix} \lambda_{1} & \lambda_{2} & \lambda_{3} \end{bmatrix}$
$\mu = \begin{bmatrix} \mu_{1} & \mu_{2} \end{bmatrix}$

Subtitute all of these term into HJBE

\begin{align*} H(x,u,\lambda,\mu) &= \sum_{k=0}^{N-1}(x_{k}-x_{k,ref})^{T}Q(x_{k}-x_{k,ref}) + (u_{k}-u_{k,ref})^{T}R(u_{k}-u_{k,ref}) + (x_{N}-x_{N,ref})^{T}Q(x_{N}-x_{N,ref}) \\ & + \begin{bmatrix} \lambda_{1} \\ \lambda_{2} \\ \lambda_{3} \end{bmatrix}^{T} \begin{bmatrix} u_{1}*\cos(\phi) \\ u_{1}*\sin(\phi) \\ u_{2} \end{bmatrix} + \begin{bmatrix} \mu_{1} \\ \mu_{2} \end{bmatrix}^{T} \begin{bmatrix} \left(u_{1}-\frac{u_{1max}+u_{1min}}{2}\right)^{2}+u_{1dummy}^{2}-(\frac{u_{1max}-u_{1min}}{2})^{2} \\ \left(u_{2}\frac{u_{2max}+u_{2min}}{2}\right)^{2}+u_{2dummy}^{2}-(\frac{u_{2max}-u_{2min}}{2})^{2} \end{bmatrix} \end{align*}

By doing partial derivative of HJBE, we get

Hamiltonian respect to states
$\frac{\partial H}{\partial x}$

\begin{equation*} \frac{\partial H}{\partial x} = \begin{bmatrix} (x-x_{ref})q_{1} \\ (y-y_{ref})q_{2} \\ (\phi-\phi_{ref})q_{3} - \lambda_{1}\sin{(\phi)}u_{1} + \lambda_{2}\cos{(\phi)}u_{1} \end{bmatrix} \end{equation*}

Hamiltonian respect to input control
$\frac{\partial H}{\partial x}$

\begin{equation*} \frac{\partial H}{\partial u} = \begin{bmatrix} (u_{1}-u_{1,ref})r_{1}+\lambda_{1}\cos{(\phi)}+\lambda_{2}\sin{(\phi)} \\ (u_{2}-u_{2,ref})r_{2}+\lambda_{3} \end{bmatrix} \end{equation*}

I know this is quite complicated, this is just only input control without constraint and solver with single shooting method.

Implementing in Python

It is safe to say that you will need to start from basic first. Like creating class for model representation, but for now I will just go with CGMRES implementing only, since I have done many demonstration of how to create class for model.

Let's create class for Hamiltion Jacobian Bellman Equation which we already derived from above equation.

class HJBEquation:

    def __init__(self, q1, q2, q3, r1, r2, u_max, u_min):

        self.q1 = q1
        self.q2 = q2
        self.q3 = q3

        self.r1 = r1
        self.r2 = r2

        self.u1_min = u_min[0]
        self.u2_min = u_min[0]

        self.u1_max = u_max[0]
        self.u2_max = u_max[1]

    def dhdx(self, x, y, yaw, x_r, y_r, yaw_r, u1, lam1, lam2):

        dhdx1 = (x-x_r)*self.q1
        dhdx2 = (y-y_r)*self.q2
        dhdx3 = (yaw-yaw_r)*self.q3-u1*lam1*np.sin(yaw)+u1*lam2*np.cos(yaw)

        return dhdx1, dhdx2, dhdx3

    def dhdu(self, yaw, u1, u2, u1_r, u2_r, lam1, lam2, lam3, mu1, mu2):

        dhdu1 = self.r1*(u1-u1_r)+lam1*np.cos(yaw)+lam2*np.sin(yaw)+2*mu1*u1*(u1+(self.u1_max+self.u1_min)/2)
        dhdu2 = self.r2*(u2-u2_r)+lam3+2*mu2*(u2+(self.u2_max+self.u2_min)/2)

        return dhdu1, dhdu2

    def dphidx(self, x, y, yaw, x_r, y_r, yaw_r):
        dphidx1 = self.q1*(x-x_r)
        dphidx2 = self.q2*(y-y_r)
        dphidx3 = self.q3*(yaw-yaw_r)

        return dphidx1, dphidx2, dphidx3

Here, I suggest that you should understand the mathematics equations above that I try to explain. It is easy to do it in Python programming language if you already understand its expression. Now I created another class for NMPC with CGMRES .

class NMPCCGMRES:

    def __init__(self):

        ## NMPC params
        self.x_dim = 3
        self.u_dim = 2
        self.c_dim = 2
        self.pred_horizons = 10

        ### Continuations Params
        self.ht = 1e-5
        self.zeta = 1/self.ht
        self.alpha = 0.5
        self.tf = 1.0

        ### Matrix

        self.q1 = 1
        self.q2 = 6
        self.q3 = 1
        self.r1 = 1
        self.r2 = 0.1

        ### Constraint
        self.u_min = [ 0,  0]
        self.u_max = [ 2,  1.57]
        self.u_dummy = [0.01, 0.01]

        ### Initialize matrix solution
        self.dU = np.zeros((self.u_dim, self.pred_horizons))

        ### Reference point
        self.X_r = [3, 2, 0.0]
        self.U_r = [0, 0]

These are just for tuning parameters and initialize parameters, let's focus on CGMRES method. As the expression above at equation (1). Let's denote that

X = np.zeros((x_dim, pred_horizons+1))      ## State for N-prediction+1
U = np.zeros((u_dim, pred_horizons))        ## Input Control for N-prediction
Lambda = np.zeros((x_dim, pred_horizons+1)) ## Costate vector for N-prediction+1
dt = 0.01                                   ## Sampling Time

Then, we can perform equation (1) as

def calc_state(self, X, U, dt):

        for i in range(self.pred_horizons):
            x_dot, y_dot, yaw_dot = self.robot_model.forward_kinematic(X[2, i], U[0, i], U[1, i])
            
            X[0, i+1] = X[0, i] + x_dot * dt
            X[1, i+1] = X[1, i] + y_dot * dt
            X[2, i+1] = X[2, i] + yaw_dot * dt

        return X

Next we calculating costate, we are going in backward direction

def calc_costate(self, X, U, Lambda, dt):

        x_N, y_N, yaw_N = self.hjb_equation.dphidx(X[0, -1], X[1, -1], X[2, -1],
                                                   self.X_r[0], self.X_r[1], self.X_r[2])
        Lambda[0, -1] = x_N
        Lambda[1, -1] = y_N
        Lambda[2, -1] = yaw_N


        for i in reversed(range(1, self.pred_horizons)):

            dhdx1, dhdx2, dhdx3 = self.hjb_equation.dhdx(
                X[0, i], X[1, i], X[2, i],
                self.X_r[0], self.X_r[1], self.X_r[2],
                U[0, i], Lambda[0, i+1], Lambda[1, i+1]
            )

            Lambda[0, i] = Lambda[0, i+1] + dhdx1 * dt
            Lambda[1, i] = Lambda[1, i+1] + dhdx2 * dt
            Lambda[2, i] = Lambda[2, i+1] + dhdx3 * dt
    

        return Lambda

And finally, calculating Newton F Function

def calc_f(self, X, U, Lambda, Mu, dt):

        X_new = self.calc_state(X, U, dt)

        Lambda_new = self.calc_costate(X_new, U, Lambda, dt)

        F = np.zeros((self.u_dim, self.pred_horizons))

        for i in range(self.pred_horizons):
            dhdu1, dhdu2 = self.hjb_equation.dhdu(X_new[2, i], U[0, i], U[1, i],
                                                  self.U_r[0], self.U_r[1],
                                                  Lambda_new[0, i+1], Lambda_new[1, i+1], Lambda_new[2, i+1],
                                                  Mu[0, i], Mu[1, i])
            F[0, i] = dhdu1
            F[1, i] = dhdu2
            
        F = F.T.ravel().reshape(-1, 1)

        return F

Now let's introduce Continuation method for Function F, you can look at the Continuation part.

# Time step horizons
dt = self.tf * (1-np.exp(-self.alpha*time)) / self.pred_horizons
# F(x,u,t+h)
F = self.calc_f(X, U, Lambda, Mu, dt)
# F(x+hdx,u,t+h)
x_dot, y_dot, yaw_dot = self.robot_model.forward_kinematic(X[2, 0], U[0, 0], U[1, 0])
X[:, 0] = X[:, 0] + np.array([x_dot, y_dot, yaw_dot]) * self.ht
Fxt = self.calc_f(X, U, Lambda, Mu, dt)
# F(x+hdx,u+hdx,t+h)
Fuxt = self.calc_f(X, U + self.dU*self.ht, Lambda, Mu , dt)

# Define right-left handside equation
left = (Fuxt - Fxt) / self.ht
right = -self.zeta * F - (Fxt - F)/self.ht

Here is the crucial part, we need to implement GMRES solver for our F function to obtain solution vector.

# Define right-left handside equation
left = (Fuxt - Fxt) / self.ht
right = -self.zeta * F - (Fxt - F)/self.ht

# Define iterations
m = (self.u_dim ) * self.pred_horizons
# Define r0
r0 = right - left
# print(r0)

# GMRES
Vm = np.zeros((m, m+1))
Vm[:, 0:1] = r0 / np.linalg.norm(r0)
# print("Vm", Vm[:, 0])
Hm = np.zeros((m+1, m))
# print(Vm[:, 0])


for i in range(m):
    Fuxt = self.calc_f(
        X, U + Vm[:, i:i+1].reshape(self.u_dim, self.pred_horizons, order='F') * self.ht,
        Lambda, Mu,
        dt
    )

    Av = (Fuxt - Fxt) / self.ht

    for k in range(i+1):
        Hm[k, i] = np.dot(Av.T, Vm[:, k:k+1])

    temp_vec = np.zeros((m, 1))

    for k in range(i+1):
        temp_vec = temp_vec + np.dot(Hm[k, i], Vm[:, k:k+1])

    v_hat = Av - temp_vec

    Hm[i+1, i] = np.linalg.norm(v_hat)

    Vm[:,i+1:i+2] = v_hat/Hm[i+1, i]

e = np.zeros((m+1, 1))
e[0, 0] = 1.0
gm = np.linalg.norm(r0) * e
# print(gm)

UTMat, gm = self.ToUTMat(Hm, gm, m)

min_y = np.zeros((m, 1))

for i in range(m):
    min_y[i][0] = (gm[i, 0] - np.dot(UTMat[i:i+1 ,:] ,min_y))/UTMat[i, i]

dU_new = self.dU + np.dot(Vm[:, 0:m], min_y).reshape(self.u_dim, self.pred_horizons, order='F')

self.dU = dU_new

U = U + self.dU * self.ht

You can look in my code inside function solve_nmpc .

Experiment in Python

GMRES was consider one of the fastest solver for sparse linear algebra problem, so I will include the link for the GMRES algorithms.
In my experiment, I use differential drive robot.
Consider as our state representation

x = \begin{bmatrix} x \\ y \\ \phi \end{bmatrix}

and of course setting initialization

x_{0} = [0.0, 0.0, 0.0]

, also

u_{0} = [0.0, 0.0]

Animation of Differential Drive robot on optimal trajectory !!!

And here are the optimal data for all state and input control.

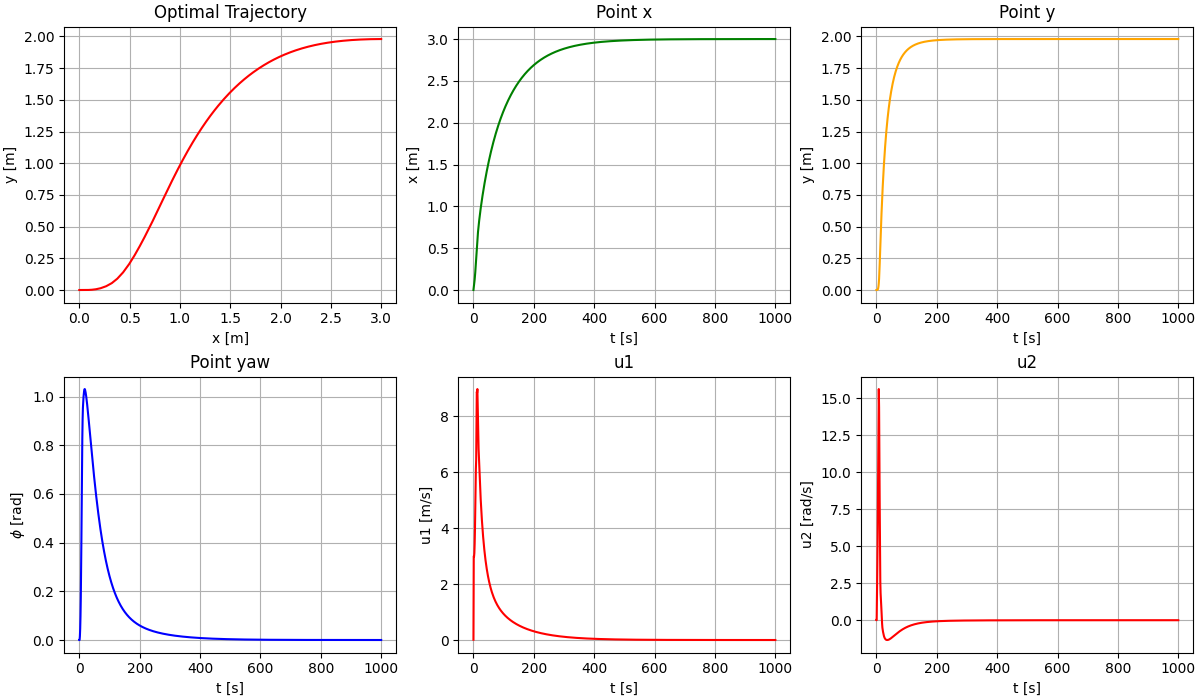
All data obtained after simulation.

You can find all the code of NMPC even with CasAdi and CGMRES here in my github: Path-Tracking

In Conclusion

Nonlinear Model Predictive Control with CGMRES is one of the great NMPC method that you should try, since it provides a very fast numerical calculation thank to the GMRES algorithms with Given Rotation method. Even though compare to another NMPC solver, NMPC with CGMRES sometime is hard for finding the optimal parameters in order to not cause unstable numerical calculation. Next time, I will bring the multiple shooting method which is consider in the promise of more robust numerical stability tha single shooting method.

Nonlinear Model Predictive Control with C/GMRES

Author: Din Sokheng